Lamport clocks are a simple technique used for determining the order of events in a distributed system. First proposed by Leslie Lamport in a paper available here, a Lamport clock maintains order of operations by incrementing a counter contained in the events. By simply adding a counter value to events as they are received and incrementing this value based on the last seen value, Lamport clocks provide a simple way to determine order of events. Lamport clocks provide a partial ordering of events – specifically “happened-before” ordering.

Example Scenarios

“Happened-before” ordering is a partial ordering of events in a distributed system. The idea is that for two given events $E_1$ and $E_2$, there exists a series of events or state changes within all of the running processes that lead from $E_1$ to $E_2$. This type of synchronization is limited – since the Lamport clock contains only basic information about the ordering of events, this clock really only has meaning when looking at the relationship of events moving between processes. The other limitation of this technique is that these clocks can only show if an event happened before another event.

An easier way to think about this is to consider two events, A and B. If A and B occur inside the same process and A is processed before B, A “happened-before” B. If A is an event sending from a process, and B is the event receiving a message on a remote process, A “happened-before” B. Lamport also defined a transitive property, where if A “happened-before” B, and B “happened-before” C, then A “happened before” C. If A “happened-before” B, then A can be said to causally affect B. For example, if A is a piece of data that a remote process needs to use to make a decision, and C is the decision event:

     P1| A ↴
     P2|   B → C

Using Lamport clocks, C can be said to have been caused or affected by A. If there is no “happened-before” relationship, then the events are considered concurrent.

As an example, of a Lamport clock, consider three processes running in a distributed system, $P_1$, $P_2$, and $P_3$. Each process starts with a Lamport clock, $L_n = 0$.

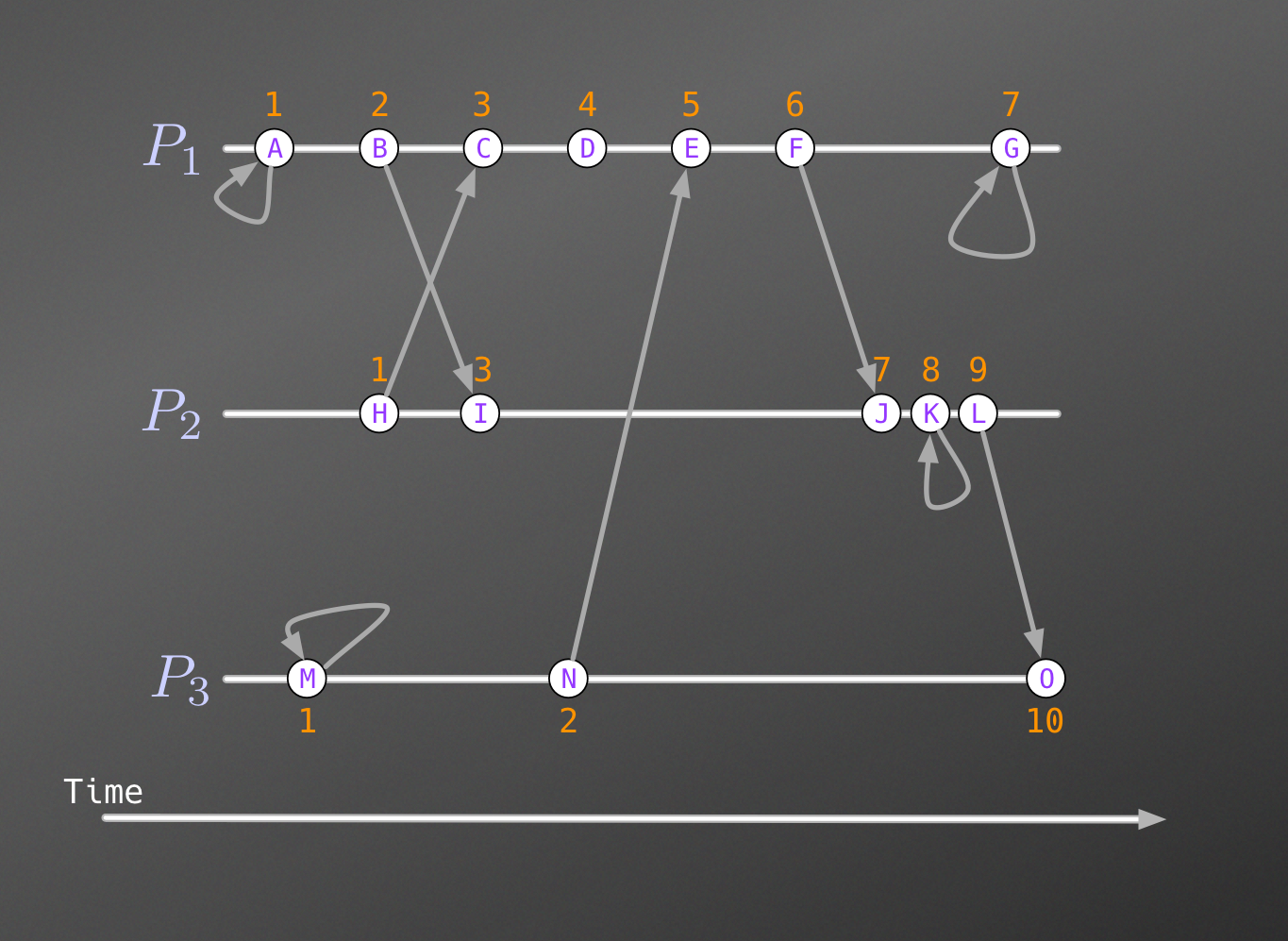
When $P_1$ processes event $A$, it increments its local clock by one. At the same time, $P_3$ processes a local event, and increments its clock by one. At this point, events $A$ and $L$ have been processed. $P_1$ and $P_3$ have a clock value of 1, and $P_2$ has a clock value of zero. Next, $P_2$ sends a message, $H$, to $P_1$ with a clock value of 1. At the same time, $P_1$ sends a message to $P_2$, with a clock value of 2. When $P_1$ receives the message from $P_2$ ($C$),  it follows the Lamport clock algorithm of:

$clock_{t1} = max(message_{clock}, clock_{t0}) + 1$

This results in $P_1$’s clock being set to 3. When $P_2$ receives the message at $I$, the clock is set to the highest value + 1 as well. Both $P_1$ and $P_2$ now have clock values of 3.

The rest of the diagram follows this algorithm. Lamport’s clocks let us know specific information about event timing, but there are some things that are not known about the system. For example, it is impossible to determine if event $L$ happened before or after event $H$. The events might be concurrent, but Lamport clocks do not provide this information. For the purposes of the Lamport clock, events $A$ and $L$ are said to be concurrent.

Furthermore, we can say that event $F$ causally affects event $N$ from this diagram. However, even though event $H$ has a clock value that is less than event $I$, we cannot say that event $H$ happened before event $I$ based solely on the Lamport clock information.

Within ROSS

While the limitation of the Lamport clock makes its use case limited, within the ROSS framework this clock can be used to find a chain of related events. Since the “happened-before” relationship is transitive the clocks can be followed backwards to find a chain of related events. In the example diagram, there is a causal chain of events starting at $F$ and ending at $O$. This means that event $F$ affected event $O$. This information provides a way to trace messages that need to be rolled-back.